Game Theory Examples (i) - Iterated Removal of Dominated Strategies
Iterated strict dominance
Iterated elimination is about removing strategies which are dominated by other ones. A player's strategy is dominated if all associated utility values (rewards) are strictly less than those of some other strategy (or a mixing of other strategies, but that can be left out for now).
Games between two players are often written in a so called game matrix. The first (row) player strategies are written as rows and the second (column) player's as columns. The utility/payoff outcome of each combination of strategies are then written in the cells of the matrix, so that the utility for the row player is the first value, and the utility for the column player is the second one.
I've marked it with colours in the example below, where the row player strategies and utilities are marked in blue, while the column player uses black.
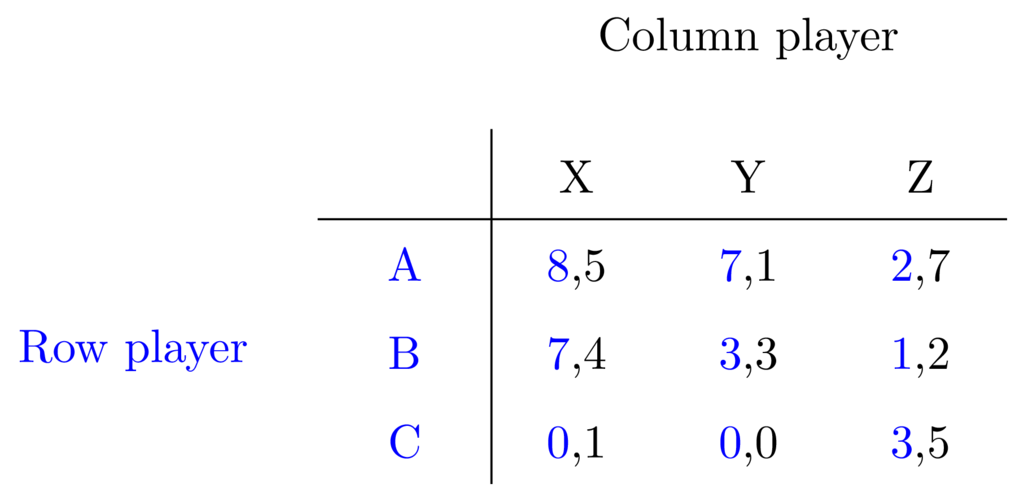
Here the row player has three choices: A, B, or C, while the column player has three other: X, Y, or Z. In (basic) game theory the players are often assumed to be perfectly rational and self-interested: they want to do as well as possible for themselves, and don't care for others. Based on that we can ask if it is possible to exclude one or more of the strategies for one or both of the players, and in process simplify the possible outcomes. When one strategy is removed further simplification may become feasible, and so the whole process can be iterated.
Finding dominated strategies
To find dominated strategies - those which may be removed - we have to compare the utility values for the strategies for the respective player. Let's do that for the matrix above.
The Row player can choose any of the rows, and their utility is the first of each pair of values. First, compare A (values \(8,7,2\)) and B (values \(7,3,1\)): \(8 > 7\), \(7 > 3\), \(2 > 1\). Well, row B is smaller than A in every column. We say that A dominates B: If you think about it, this means that whatever strategy (X, Y, or Z) picked by the Column player, if the Row player has to choose between A and B - it is always better to choose A!
So we found one dominated strategy. Let's continue. A vs C : \(8 > 0\), \(7 >0\), \(2 <3\). So here with see that two components of A is greater than C but one is not. Therefore neither does A dominate C, nor does C dominate A.
Then B vs C: \(7 > 0, 3 >0, 1<3\) - neither of them dominates the other.
The Column player can choose between X,Y, Z. So, now we compare the second values against each other for every column.
X vs Y : \(5>1, 4 > 3, 1 > 0\); so every value of X is greater than the corresponding value of Y. This means that X dominates Y. (Because for the column player it is always better to choose X over Y no matter what the row player does.)
X vs Z : \(5 < 7, 4 > 2, 1 < 5\) - no dominance for either strategy.
Y vs Z : \(1 < 7, 3 >2, 0 < 5\) - again no dominance.
Removal of dominated strategies
When we have found one or more dominated strategies these can be discarded from the game.
As we have found two of them in this iteration you may ask 'will it matter which one is removed first?'
The answer is no, as long as there is a strict dominance. That is, the utility values of a dominated strategy must always be strictly less than those of the dominating one. (If all values are only less or equal it is called weak dominance and then the order can matter [so be careful!].) Here, we are only concerned with strict dominance.
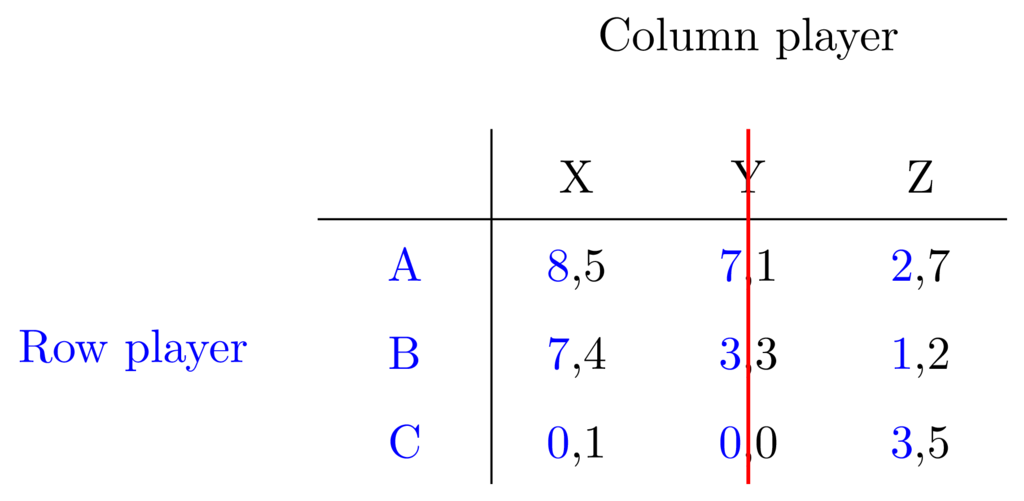
Anyway, let's just cross out the dominated strategies from the table.
First Y:
Then B:
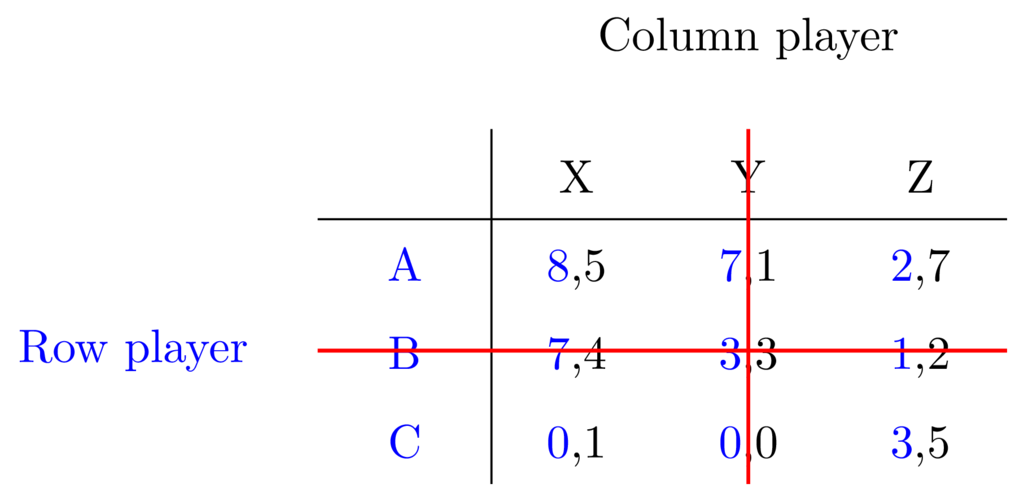
Now we are left with a simplified matrix, and can iterate the algorithm comparing the remaining utilities in the same way.
So compare A and C again: \(8 >0, 2 < 3\). Still no dominance here.
Then compare X and Z: \(5 < 7, 1 < 5\). Aha, so now Z dominates X. It didn't before, but as the row player has discarded strategy B, the need for that comparison is gone. So, column X can be removed:
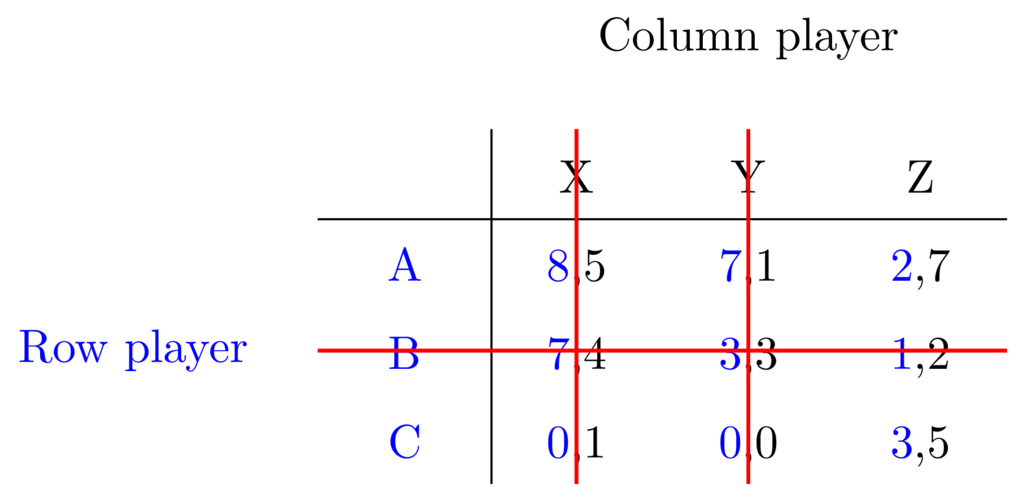
Next iteration - we are left with in effect a 2x1 matrix. There is no choice left for the column player - it will always be best for them to choose strategy Z, but the row player may still pick either A or C. So, let's take this for another round and compare A and C: \(2 < 3\). So, this time around C dominates A, meaning this too can be removed:
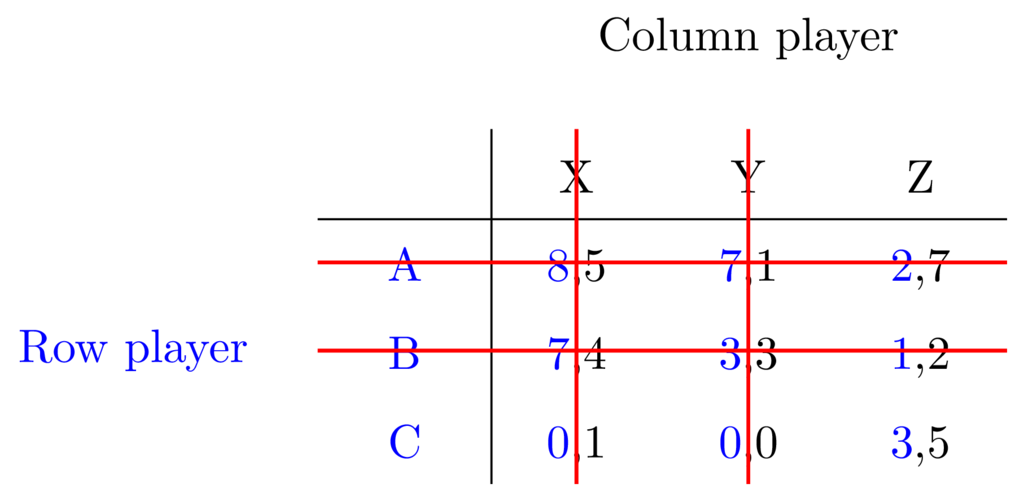
We are now left with a single cell, and the knowledge that the optimal strategy for the Row player is C and the optimal strategy for the column player is Z. The associated utility is 3 for the Row player, and 5 for the Column player.
If you look at that reward you can see that no player is able to do better on their own. That is, the Row player would not rather choose A or B (given that the column player has chosen Z) and the column player would not rather choose X or Y (given that the row player has chosen C). (Sure, there are better rewards elsewhere, but that would require both players to agree to change, and once there at least one player can get an ever better reward by choosing something else.)
This is iterative elimination which is used to simplify games. Note that this time it took us all the way to a specific combination of strategies which isn't always the case. Often you may be left with multiple strategies per player.
Nota bene
The basis for this document is a game theory exercise session I taught for an AI course. The notes are quite verbose to start with, because I'm trying to explain every step extensively. Moreover some terms are not directly defined even though I try to explain things on a quite basic level. It was assumed that the students had attended an introductory lecture. So the game is on normal form, 'equilibrium' means Nash equilibrium, and so on. Also please note that in the text I use the terms reward, payoff, and utility interchangeably.
Basically, this is an in-depth example, not a formal introduction.